Одним из путей изучения генетики панмиктической популяции является исследование характера и частоты распространения в ней особей, гомозиготных и гетерозиготных по отдельным генам.
Представим, что в какой-то популяции число форм, гомозиготных по разным аллелям одного гена, т. е. форм АА и аа, одинаково. Такая популяция будет производить равное число как мужских, так и женских гамет с этими аллелями: 0,5А и 0,5а.
Если особи, носители данных аллелей, свободно скрещиваются между собой, то встреча гамет при оплодотворении является случайным событием, в результате чего возможны следующие комбинации:
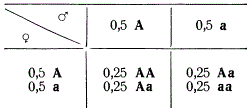
Нетрудно заметить, что в данном поколении (F1) доминантные гомозиготы АА будут возникать с частотой 0,25, гетерозиготы Аа — с частотой 0,50 и гомозиготы по рецессивной аллели аа — с частотой 0,25. В следующем поколении при тех же условиях равновероятного образования гамет в мейозе и свободного скрещивания частота гамет с доминантной аллелью А будет равной 0,5 (0,25 от доминантных гомозигот АА + 0,25 от гетерозигот Аа). Частота гамет с рецессивной аллелью а составит также 0,50 (0,25 от гомозигот аа + 0,25 от гетерозигот Аа). Относительная частота образования разных генотипов популяции вновь будет 0,25 АА: 0,50 Аа: 0,25 аа. Отсюда следует, что в каждом поколении относительная частота гамет с доминантной и рецессивной аллелями гена сохраняется на одном уровне: 0,5 А и 0,5 а.
Однако популяция в огромном большинстве случаев состоит из разного числа гомозигот АА и аа: одних может быть больше, чем других. Разберем следующий пример.
Для человека известен доминантный ген Т (Taster—дегустатор). Носитель его обладает свойством определять на вкус слабый раствор фенилтиокарбамида как горький. Обладатель рецессивной аллели этого гена в гомозиготном состоянии (tt) тот же раствор определяет как безвкусный.
Представим себе некую популяцию людей, живущих в изолированном районе, где браки происходят в основном между жителями этого района и сочетание в отношении данного гена совершается чисто случайно.
Если в какой-то выборке соотношение гомозиготных и гетерозиготных лиц — «дегустаторов» (Т —) и «недегустаторов» (tt) — не равное, а, допустим, «недегустаторов» оказалось примерно в два раза больше, чем «дегустаторов» (~1,8 tt : 1 Т —), то в соответствии с этим соотношение частот аллелей в популяции будет не 0,5 t : 0,5 Т, а порядка 0,80 t : 0,20 Т. Поскольку бракосочетания между носителями данного гена будут случайными, то мы вправе ожидать в потомстве на каждые 100 зигот 4% гомозиготных и 32% гетерозиготных «дегустаторов» и 64 % «недегустаторов».
Что же можно ожидать в следующем поколении? Гаметы с аллелью Т будут возникать с частотой 0,20 (0,04 от гомозиготных ТТ + 0,16 от гетерозиготных Tt «дегустаторов»). Гаметы с аллелью t будут возникать с частотой 0,80 (0,64 от tt 0,16 от Tt). Отсюда следует, что в указанной популяции при тех же условиях поддерживается одинаковое соотношение частот генотипов (0,2Т : 0,81) и фенотипов (64% «недегустаторов» и 36% «дегустаторов»). Такое соотношение повторяется в каждой последующей генерации. В этом случае популяция находится в равновесии по данному гену.
В 1908 г. двумя авторами, математиком Г. Гарди в Англии и врачом В. Вайнбергом в Германии, независимо друг от друга была предложена формула, отражающая распределение генотипов и фенотипов в популяции, получившая название формулы Гарди — Вайнберга. Гарди и Вайнберг исходили из того, что при определенных условиях, не изменяющих частоту аллелей, популяции имеют определенное соотношение особей с доминантными и рецессивными признаками, а относительные частоты каждой аллели имеют тенденцию оставаться постоянными в ряду поколений.
Если частоту встречаемости одной из аллелей в гаметах, допустим Т, обозначить через q, тогда частота другой аллели t будет 1 — q. тогда в потомстве будут следующие отношения:
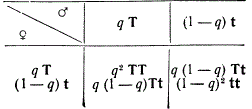
Произведя суммирование этих данных, получим формулу Гарди — Вайнберга, отражающую распределение генотипов и фенотипов в популяции:
Формула Гарди — Вайнберга
Нетрудно заметить, что это выражение представляет разложение бинома [qT + (1 — q) t]2, который для общего случая будет [qA + (1 — q)a]2.
Указанная формула позволяет рассчитывать относительную частоту появления генотипов и фенотипов в популяции. Их пропорция будет оставаться для данной панмиктической популяции постоянной в ряду поколений при отсутствии отбора. Но определение частоты появления гамет с той или иной аллелью гена непосредственно из фенотипических частот возможно лишь при наличии неполного доминирования. В случае же полного доминирования такой подсчет невозможен, и поэтому исходят из частоты фенотипического класса рецессивных гомозигот в популяции. При этом предполагают, что распределение частот генотипических классов в популяции соответствует формуле Гарди — Вайнберга. Пусть, например, в популяции крупного рогатого скота обнаружено, что рогатые животные встречаются с частотой 25% или 0,25, а комолые — с частотой 75% или 0,75. Комолость определяется доминантным состоянием гена А, рогатость — его рецессивной аллелью а, причем имеет место полное доминирование.
Следовательно, на основе учета частоты определенных фенотипов в популяции можно составить представление о распределении в ней соответствующих генотипов. Указанный расчет производится 1) для одной пары аллелей, но не для многих членов серии множественных аллелей, 2) для аутосомных генов, но не для генов, сцепленных с полом. Во всех этих случаях расчеты производят исходя из известного условия, что сумма частот аллелей гена равна 1.
Следует отметить особенности в наступлении равновесия по генам, локализованным в половой хромосоме. Дело в том, что при случайном скрещивании равновесие здесь не достигается в одном поколении, поскольку Х-хромосомы не свободно комбинируются среди всего потомства, как это имеет место для генов в аутосомах. Распределение Х-хромосом происходит по типу крис-кросс (от отца к дочерям, от матери к сыновьям). Поэтому по этим генам равновесие генотипов в панмиктической популяции наступает только через несколько поколений. Однако частоту рецессивного гена, локализованного в половой хромосоме, легко установить непосредственно по распределению фенотипов среди особей гетерогаметного пола. Возвращаясь к общей оценке всех расчетов частоты аллелей гена в генофонде и частоты генотипов в панмиктической популяции, следует помнить, что сама формула Гарди — Вайнберга пригодна лишь для относительно простых случаев анализа генетики популяций. Как правильно указывают генетики, принцип расчета по формуле отражает лишь статику популяции, но не ее генетическую динамику. При этом надо также помнить, что частота фенотипа, определяемого данным геном, зависит как от частоты самого гена в генофонде популяции, так и от его свойств — доминантности или рецессивности, пенетрантности и экспрессивности.
Рассмотренная нами формула применима для расчетов при следующих условиях: 1) если спаривание особей и сочетание гамет в популяции совершаются случайно, т. е. при отсутствии какой бы то ни было избирательности; 2) если мутации от доминантной аллели к рецессивной и обратно происходят настолько редко, что их частотой можно пренебречь; 3) если обследуемая популяция многочисленна, так что случайность выборки не имеет существенного значения; 4) если особи, гомозиготные и гетерозиготные по паре аллелей данного гена, имеют одинаковую жизнеспособность, плодовитость и не подвергаются отбору. Очевидно, что эти условия далеко не всегда осуществляются в природных популяциях, ограничивая тем самым приложение формулы Гарди — Вайнберга. Несмотря на это, данное в формуле выражение генетических отношений способствует пониманию отдельных генетических явлений, имеющих место в популяции свободно скрещивающихся организмов.
Знание частоты распространения некоторых наследственных признаков в человеческом обществе позволяет рассчитывать частоту мутантных генов (их концентрацию), например частоту аллелей групп крови, резус-фактора и др. Зная распространение отдельной летальной мутации у крупного рогатого скота, овец или свиней в определенном районе, можно рассчитывать вероятность встречаемости ее в гомо- и гетерозиготном состоянии.
Изучение распространения генов в популяции позволяет следить за накоплением в ней вредных (летальных) мутаций, что особенно важно при повышении фона радиации, а также при применении различных препаратов в корме для животных и различных химических удобрений для растений.
Указанные расчеты имеют значение и для селекционера при поисках в популяции ценных качеств, определяемых отдельными мутантными генами.
