В XX веке исследователи завершили построение основной теории поверхностных волн установившегося типа в идеальной жидкости, т. е. жидкости, в которой малы силы внутреннего трения.
Особо велик вклад в эту область науки, сделанный А. И. Некрасовым, Н. Е. Кочиным, Л. Н. Сретенским: их работы позволили перейти от динамики волн весьма малой высоты к динамике волн, высота которых сравнима с длиной — составляет несколько сотых от длины волн.
Требования практики заставляют продолжать теоретические исследования дальше, искать решение весьма трудных задач о волнах неустановившегося типа в реальной жидкости, обладающей значительным внутренним трением турбулентного происхождения. Приходится ставить специальные опыты в новых лабораторных условиях, близки к природным условиям зарождения, распространения и гашения морских волн.
Широкие возможности открылись перед советскими исследователями после вступления в строй «штормового бассейна», построенного по идее автора в Черноморском отделении Морского гидрофизического института Академии паук СССР. Это — бассейн в форме кольца, с внешним диаметром 40 м, шириной пространства между стенками 2 м и высотой 5 м. Нижние 2,5—3 м заполняются морской водой, а вдоль кольцевого канала над водой посредством мощных центробежных насосов создается непрерывный воздушный поток. Скорость ветра здесь может достигать 19 м/сек, т. е. по шкале Бофорта 9 баллов. Удобнее всего вести опыты при скоростях ветра до 13 м/сек, когда дольше сохраняются условия, близкие к природным: дольше не сказывается влияние трения о стенки бассейна или сказывается так мало, что его можно исключить путем надежных вычислений.
Сперва на гладкой поверхности воды в кольце появляется мелкая рябь капиллярных волн; затем мелкие волны нарастают в высоту и несколько медленней в длину; на некоторой стадии достигается максимум крутизны волн — максимум отношения высоты волн к их длине (его численное значение составляет 0,143). После этого наступает главный этап развития ветровых волн, на котором увеличение длины волн идет быстрее, чем увеличение их высоты; в результате крутизна волн постепенно уменьшается. За всеми этими явлениями удобно наблюдать сквозь застекленную часть стенок бассейна, занимающую одну шестую его окружности. Столь же удобно фотографировать волны из центра кольца, посредством весьма длиннофокусного аппарата.

Профили мертвой зыби, ветровой волны и волны, разрушающейся под действием мелководья
На рисунке видны три характерных снимка волн. На верхнем представлены волны, сфотографированные через несколько минут после того, как были выключены воздуходувки и прекратился ветер в кольцевом канале. Это — мертвая зыбь, волны которой сохраняются в море очень долго после прекращения шторма и свободно распространяются на большие расстояния. Профиль волн очерчен по трохоиде — кривой, у которой и вершины и подошвы напоминают отрезки синусоид, но подошвы более растянуты по сравнению с вершинами.
Снимок посредине запечатлел волны, находящиеся под действием ветра (в прямом смысле — ветровые волны). Здесь отчетливо видно отличие от профиля мертвой зыби: подошва еще более растянута, чем у трохоиды, а на заострившейся вершине возникло ребро, которое свидетельствует о достижении крутизны, предельной в заданных условиях.
Еще в прошлом веке английский гидродинамик Митчел показал, что даже без воздействия ветра может возникнуть на вершине волн такое ребро, при предельном отношении высоты волн к длине, равном 1/7. Причина возникновения этого — критического — состояния не рассматривалась в цитированной работе.
Опыты в штормовом бассейне и теоретический анализ их результатов позволили найти физическую причину заострения вершин волн до появления ребра и причину их разрушения после такого критического состояния. Оказалось, что в основе всех этих интересных явлений лежит пульсация скоростей течений, возникающих одновременно с волнением.
Еще английский математик Стокс в прошлом веке показал, что даже при отсутствии ветра частицы воды на волне описывают не замкнутые окружности, как предполагалось прежде, а своеобразные петли: на круговое движение частиц налагается слабое поступательное движение их, направленное в сторону распространения волн. И сам Стокс, и последующие авторы считали скорость такого «волнового течения» постоянной. Однако в действительности скорость стоксова течения пульсирует около средней величины, достигая максимума у подошвы волн и уменьшаясь до нуля на вершинах. Колебания скорости тем значительней, чем больше отношение высоты волн к длине. При действии ветра на стоксово течение налагается течение дрейфовое, которое пульсирует по тому же закону, но с еще большей амплитудой. Вот почему при сильном ветре на вершинах волн очень рано (значительно ранее крутизны 1/7) возникают острые гребни, ежесекундно готовые обрушиться. Именно так создаются на волнах — при больших скоростях ветра — хорошо известные пенистые «барашки».
Столь же подробно удалось исследовать разрушение вершин волн по другой причине — под действием мелководья; было показано, что фазовая скорость волн не остается постоянной, а достигает максимума на вершине волн и минимума — 1/7 подошвы. Были вычислены профили мертвой зыби и профили метровых волн, искаженных при движении на мелководье, и определены условия разрушения вершин волн, потерявших устойчивость вследствие искажения. Нижний снимок дает представление о том, каким становится профиль волн, искаженный под действием мелководья, — перед самым разрушением вершины волны.
Для практических целей мореплавателей и портостроителей очень важно научиться вычислять размеры волн, которые могут возникнуть через заданный срок действия ветра заданной скорости, на заданном расстоянии от того берега, с которого дует ветер. Вероятно, невозможно — да и не нужно — решать эту задачу, исходя из уравнений движения жидкости. Поэтому еще в 1937 году В. В. Макавеев предложил решать ее на основе закона сохранения энергии.
Энергия волн в каждый момент времени пропорциональна квадрату их высоты. Отсюда следует, что мощность, расходуемая на увеличение высоты волн, пропорциональна скорости нарастания высоты. Эта мощность черпается, у ветра, воздействующего на волны, но, кроме того, ветер обязан покрыть расход мощности на преодоление внутреннего трения в воде, возрастающею при увеличении высоты волн. Постепенно эти потери становятся все значительней и значительней, а потому скорость нарастания высоты волн постепенно уменьшается. Предельная высота волн, возможная при заданной скорости ветра, определяется тем, что мощность, передаваемая волнам от ветра. полностью расходуется на преодоление сил внутреннего трения в воде.
Двадцать три года назад, когда возникла эта первая схема вычисления размеров волн, и в последующие десятилетия оставался неизвестным действительный механизм передачи энергии ветра волнам. Выяснилось, что питание волн энергией ветра безусловно зависит от крутизны волн, т. е. от отношения их высоты к их длине; но не был известен закон, по которому нарастает длина волн, и даже сама причина нарастания их длины.
Лишь в 1954—1955 годах опыты и теоретические исследования, проведенные автором, показали, что ветер как бы «нагнетает» энергию в волны, давя на поверхностные частицы воды с большей силой, когда они опускаются, и с меньшей силой, когда они поднимаются при волновом движении. «Нагнетаемая» мощность пропорциональна квадрату разности между скоростью ветра и фазовой скоростью волн, высоте волн и их крутизне.
Очень просто разрешилась задача о нарастании длины волн, как только к исследованию была привлечена классическая теорема о моменте количества движения почему-то не применявшаяся прежде в гидродинамике и впервые примененная Н. Е. Жуковским к исследованию движения твердых тел с полостями, содержащими жидкость). По этой теореме прирост момента количества движения в единицу времени равен моменту всех действующих внешних сил. Напомним, что момент количества движения какой-то массы равен произведению этой массы на скорость движения и на длину перпендикуляра, опущенного из «центра моментов» на направление движения в данное время. Моментом силы называется произведение силы на перпендикуляр, опущенный на ее направление из той же точки.
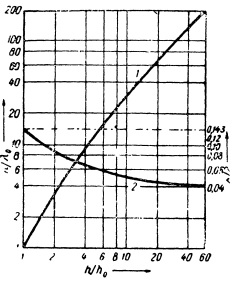
Нарастание длины волн и уменьшение их крутизны
Обнаружилось, что длина волн нарастает под действием ветра именно потому, что нарастает момент количества движения водных частиц, движущихся по их траекториям. Сам закон нарастания представлен на рисунке, причем для удобства применена логарифмическая сетка: по осям фактически отложены не величины, а их логарифмы, и потому диаграмма заняла мало места. Величина h/h0 представляет собой отношение высоты волн в данный момент времени к высоте волн на той стадии, когда они обладали наибольшей крутизной; величина λ/λ0 — отношение длины волн в данный момент к длине волн на стадии наибольшей крутизны. Кривая 1 на рисунке показывает, что при увеличении высоты волн в 4 раза длина их возрастает почти в 9 раз; при увеличении высоты волн в 8 раз — длина возрастает более чем в 20 раз; при увеличении высоты волн в 60 раз — длина возрастает более чем в 200 раз. Именно поэтому непрерывно падает крутизна волн по закону, описанному кривой 2 на том же рисунке: наибольшая крутизна равнялась 0,143; при неограниченном нарастании h/h0 крутизна стремилась бы к значению 0,04. Последующие работы автора показали, что в действительности крутизна волн стремится к значению 1/23.
Штормовой бассейн позволил открыть тонкие детали волнового движения и разобраться в энергетике волнообразования, развития волн на тех этапах, на которых практически не сказывалось влияние трения о стены или это влияние могло быть учтено. Для завершения теории ветровых волн были использованы измерения высот и длин волн в условиях океана и глубоких морей, в частности работы автора на экспедиционном судне «Седов» в Атлантическом океане в 1957 году.
На основании исследований многих авторов можно считать, что предельная высота волн в океане, возможная при заданной скорости ветра, пропорциональна квадрату этой скорости.
С другой стороны, она должна быть пропорциональна квадрату разности скоростей ветра и волн на конечной стадии. Отсюда следует, что при всякой скорости ветра предельная фазовая скорость волн может составлять только совершенно определенную долю от соответствующей скорости ветра, — именно 0,82.
Все эти соотношения дали возможность построить простые рабочие диаграммы для расчета размеров волн по заданной скорости ветра, времени его действия на волны и заданному расстоянию от той границы штормовой области в океане, со стороны которой дует ветер (в частном случае — расстоянию от берега, с которого дует ветер, — наветренного берега).
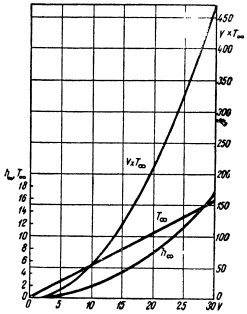
Основные параметры ветровых волн
На рисунке представлена одна из этих диаграмм, построенная применительно к скоростям ветра до 30 м/сек. Через h∞ обозначена предельная возможная высота ветровых волн в океане при соответствующем ветре V, на чрезвычайно большом расстоянии от границы шторма; через Т∞ —предельное значение периода таких волн; величина VT∞ также нужна для расчетов.
Сопоставление теоретических расчетов по методу автора с данными непосредственных измерений волн в глубоких морях и в океане дало хорошие результаты.
В настоящее время необходимо на основе этой физической теории развить статистику элементов волн при сложном и неоднородном волнении, наблюдающемся в природных условиях. При этом надо помнить, что на различных этапах развития волн совсем неодинакова вероятность отклонения волн от средних; совсем неодинакова вероятность перехода от двумерных волн, бегущих правильными параллельными рядами, к трехмерным волнам в форме «холмов» на поверхности моря. Теория показывает, что на первых этапах развития волн быстрее всего нарастает высота их на тех участках первоначально правильного «фронта», на которых возникли случайные возвышения над средним уровнем гребня; нарастание задерживается там, где случайно оказалось понижение гребня по сравнению со средней его высотой. Такая неустойчивость приводит к дроблению рядов волн на отдельные «холмы» и в то же время делает непостоянными высоты волн, бегущих одна вслед за другой.
Иная картина должна возникать на поздних этапах развития волн: теория показывает, что потери энергии на турбулентное внутреннее трение возрастают пропорционально кубу высоты волн. Следовательно, по мере приближения высот волн к установившимся значениям заметнее всего будет замедляться нарастание высот волн там, где они велики, и меньше будет замедляться там, где они малы. В результате будет постепенно сглаживаться неравенство высот в различных частях бывшего «фронта» и неравенство высот между волнами, бегущими одна вслед за другой. По этой причине самые большие штормовые волны в океане снова приобретают правильную двумерную форму: мощная штормовая зыбь бежит правильными рядами, и только на поверхности основных валов этой штормовой зыби громоздятся сложные трехмерные холмы волн — вторичных, третичных и более высоких порядков.
Совсем правильны ряды мертвой зыби, остающейся в океане после прекращения шторма и обладающей весьма большой жизнеспособностью. Иногда такая зыбь распространяется в океане далеко за пределами штормовой области, причем длина ее волн может непрерывно возрастать, достигая громадных размеров, в то время как высота волн постепенно уменьшается.
Теория ветровых волн сейчас разработана не только для условий океана, глубокого моря, но и для совсем иных условий весьма резко выраженного мелководья. Здесь снова сослужил большую службу штормовой бассейн, а выводы из опытов в нем были тщательно проверены А. П. Хваном в настоящей «природной лаборатории» — на озере Белом, почти правильной круглой формы, с диаметром около 40 км и постоянной глубиной около 3—3,5 м.
